Backtracking is a process where steps are taken towards the final solution and the details are recorded. If these steps do not lead to a solution some or all of them may have to be retraced and the relevant details discarded. In theses circumstances it is often necessary to search through a large number of possible situations in search of feasible solutions. This trial and error process is illustrated here by a discussion of a particular
problem, that of the eight queens.
In the Eight Queens problem the challenge is to place eight queens pieces
from the game of Chess on a chessboard so that no queen piece is threatening
another queen on the board. In the game of chess the queen is a powerful
piece and has the ability to attack any other playing piece positioned
anywhere else on the same row, column, or diagonals. This makes the
challenge quite tricky for humans who often declare after several failed
attempts “…there can’t be any solution!”. However there are in fact
ninety-two valid solutions to the problem although many of those ninety-two
are symmetrical mirrors. All of the solutions can be found using
a recursive backtracking algorithm. The algorithm works by placing queens
on various positions, adding one at a time until either eight queens have
been placed on the chess board or less than eight queens are on the board
but there are no more safe positions left on the board. When
the latter situation is reached the algorithm backtracks and tries another
layout of queens.
 |
-
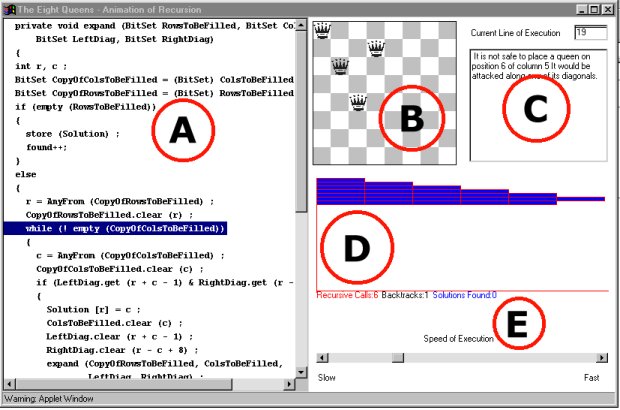
In area (A) the Java source code for the recursive backtracking algorithm
used to solve the Eight Queens is displayed. As the algorithm executes
the current line of execution is highlighted.
-
This animation shows pictorially how the chess board appears at each stage
during the search. When the algorithm tries a position for a queen the
animation updates showing the new locations for all the queens placed at
that point in time. When a solution is found it is highlighted in
the animation window in red and the execution pauses to display the solution
for a period of time.
-
Gives a textual explanation of the line currently under execution
in (A). Use the speed control bar (E) to slow down the algorithm
so that you can read each message and follow the "code walk through" at
your own pace.
-
This shows the level of recursion, In this backtracking problem the level
expands and contracts as different solutions are tried and then rejected.
The symmetry clearly visible in the simple recursive problems is not present
here.
-
This speed control allows you to speed up and slow down the rate at which
the algorithm executes.
|
|
Recursive Method To solve Eight Queens Problem in Java.
/** Recursive 8 Queens Solution.
* @author John McHugh
*/
private void expand (BitSet RowsToBeFilled, BitSet ColsToBeFilled,
BitSet LeftDiag, BitSet RightDiag)
{
int r, c ;
BitSet CopyOfColsToBeFilled = (BitSet) ColsToBeFilled.clone () ;
BitSet CopyOfRowsToBeFilled = (BitSet) RowsToBeFilled.clone () ;
if (empty (RowsToBeFilled))
{
store (Solution) ;
found++;
}
else
{
r = AnyFrom (CopyOfRowsToBeFilled) ;
CopyOfRowsToBeFilled.clear (r) ;
while (! empty (CopyOfColsToBeFilled))
{
c = AnyFrom (CopyOfColsToBeFilled) ;
CopyOfColsToBeFilled.clear (c) ;
if (LeftDiag.get (r + c - 1) & RightDiag.get (r - c + 8))
{
Solution [r] = c ;
ColsToBeFilled.clear (c) ;
LeftDiag.clear (r + c - 1) ;
RightDiag.clear (r - c + 8) ;
expand (CopyOfRowsToBeFilled, ColsToBeFilled,
LeftDiag, RightDiag) ;
ColsToBeFilled.set (c) ;
Solution [r] = 0 ;
LeftDiag.set (r + c - 1) ;
RightDiag.set (r - c + 8) ;
}
}
}
|
